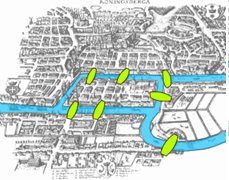
Les ponts de Konigsberg
Dans cet article, nous allons nous intéresser au problème historique dit « des ponts de Königsberg ». Il se présente de la façon suivante : « La ville de Königsberg est construite comme sur le plan ci-contre. Des ponts permettent d’enjamber la rivière pour passer d’une île à l’autre. On se demande alors s’il est possible de se balader dans la ville de sorte à partir d’un point de départ de notre choix, de passer une et une seule fois par chaque pont pour revenir à notre point de départ ».
Pour résoudre ce problème, nous allons devoir faire un détour par la théorie des graphes. Cette dernière est une branche des mathématiques à la frontière avec l’informatique. Ses applications sont aujourd’hui nombreuses : modéliser des connexions dans des réseaux (sociaux, routiers, informatiques, de télécommunications…), étudier la génétique…
Il se pourrait aussi que nous rencontrions au passage l’un des jeux auquel nous jouions étant enfant…
qu’est ce qu’un graphe ?
Concrètement, un graphe est un ensemble de points (appelés sommets), reliés ou non entre eux par ce que l’on appelle des arêtes (qui correspondent à un couple de sommets).
Vous pouvez trouver à la fin de cette section plusieurs exemples.
Un graphe peut présenter plusieurs particularités. Il peut être par exemple :
– orienté, c’est-à-dire que ses arêtes possèdent un « sens de circulation »
– connexe, il est alors constitué « d’un seul bloc ». A contrario, un graphe non connexe possèdera 2 parties indépendantes, qui ne sont connectées par aucune arrête (comme 2 îles qui ne seraient pas reliées)
– complet, si tous les sommets sont reliés entre eux.
De plus on appelle degré d’un sommet le nombre d’arêtes qui « partent » de ce sommet. On peut indiquer sur chaque sommet son degré, comme sur l’exemple suivant (qui n’est pas connexe !).
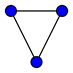
Graphe complte à 3 sommets
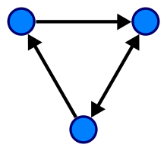
Graphe orienté
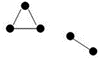
Graphe non connexe (2 morceaux non reliés)

Graphe et degré des sommets
Dessiner une maison sans lever le stylo !
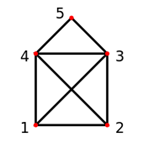
Les graphes peuvent posséder une propriété bien particulière : celle de pouvoir trouver un « chemin » qui permet de passer une unique fois par toute les arêtes (sans forcément revenir au point de départ). Un graphe possédant un tel chemin sera dit Eulérien.
Cet aspect se retrouve par exemple dans un jeu enfantin, lorsqu’il s’agit de dessiner la maison suivante sans lever le stylo !
Une question qui vient alors est la suivante « serait-il possible, en voyant un graphe, de savoir si je peux trouver un chemin qui passerait une fois par chacune de ses arêtes ? » ou encore « puis-je savoir si je peux dessiner ce graphe sans lever le stylo ? ». En fait, on veut savoir si on peut, en observant un graphe, conclure si ce dernier est eulérien !
Les plus persévérants savent bien que dans le cas de la maison, cela est possible, je vous laisse vous en convaincre !
On doit la réponse à cette question au mathématicien Euler, en 1736. Ce dernier démontre que « Un graphe connexe est eulérien si et seulement si ses sommets sont tous de degré pair, sauf au plus deux ».
Pour illustrer ce théorème, reprenons l’exemple de la maison.
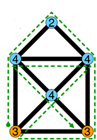
On compte 4 sommets de degré pair, et 2 sommets de degré impairs : le graphe est donc eulérien !
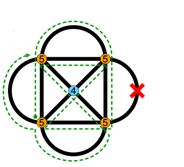
Ce graphe possède un sommet de degré pair, mais 4 sommets de degré impair : il n’est pas eulérien !
Grâce à ce théorème, vous pouvez en un coup d’œil savoir à l’avance s’il est possible de dessiner le graphe sans lever le stylo ! Mais attention, parvenir à trouver la façon de le faire peut se révéler compliqué ! Petite chose amusante : pour la maison, il existe en tout 44 façons différentes de la dessiner !
Et si on enlève le toit de la maison ? Je vous laisse comprendre pourquoi il n’est plus possible de la dessiner sans lever le crayon !

Se balader dans Konigsberg grâce à la théorie des graphes ?
Pour changer d’angle de vue quant à notre problème des ponts, nous pouvons le transformer en un problème sur les graphes. Reprenons le plan de la ville et remarquons que la rivière définit 4 zones, reliées par les 7 ponts.
Construisons alors un graphe qui modélise notre balade de la façon suivante :
– On place 4 sommets, qui correspondent aux 4 zones
– On relie 2 sommets (2 zones) par une arête uniquement si ces 2 zones sont reliées par un pont.
Finalement, un sommet correspond à une zone et une arête à un pont reliant 2 zones.
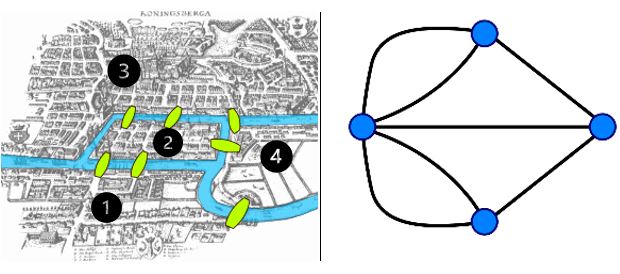
Ici, nous souhaitons faire trouver un chemin empruntant chacun des ponts. Nous voulons donc que notre graphe soit eulérien ! Mais en plus de cela, nous souhaitons arriver à notre point de départ, ce qui est encore plus fort !
Dans un graphe, un tel chemin (qui part d’un point de départ, emprunte chacune des arêtes une unique fois, et revient au point de départ) est appelé circuit eulérien.
Et c’est à nouveau Euler qui démontra comment savoir en coup d’œil si un graphe possède un circuit eulérien : « un graphe connexe admet un circuit eulérien si et seulement si tous ses sommets sont de degré pair ».
Notre graphe, qui ne possède que des sommets de degré impair ne possède donc pas de circuit eulérien ! Et nous pouvons dire adieu à notre balade dans Königsberg (enfin, il va falloir accepter d’emprunter plusieurs fois au moins un pont…).
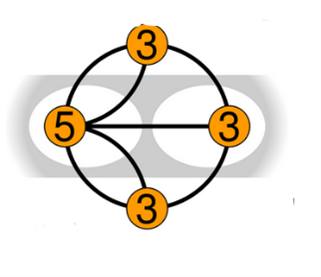
A titre d’exemple, voici un graphe eulérien (uniquement 2 sommets de degré impair) mais qui ne possède pas de circuit eulérien (car au moins un sommet de degré impair) ! Il est donc possible de le parcourir sans lever le stylo, mais il est impossible d’arriver au point de départ !
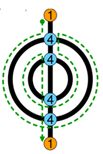
Vous voilà maintenant apte à arnaquer vos amis, en leur proposant de jouer à ce jeu « Si tu arrives en un seul essai à dessiner ce schéma sans lever le stylo, je te donne 5€. Sinon, c’est toi qui me les donnes ». Prenez le soin de prendre un graphe non-eulérien 😉.
Plusieurs images utilisées ton extraites de https://commons.wikimedia.org/wiki/File:Eulerian_path_puzzles.svg (produites par Cmglee)


Commentaires récents