Dans ce petit article, je vais vous présenter une question de dénombrement. Le dénombrement est une branche des Mathématiques qui s’occupe de … dénombrer des choses, c’est-à-dire les compter. Cela peut sembler idiot, mais parfois cela peut s’avérer très délicat. Des formules plus ou moins complexes peuvent être utilisées. Généralement le dénombrement est très peu apprécié des élèves de terminale (les combinaisons, arrangements, permutations…). Je présenterai ces notions dans de futurs articles !
Considérons un jeu de cartes complet (52 cartes). Nous allons nous demander combien existe-il de façons différentes de mélanger un tel jeu (c’est à dire compter tous les ordres de cartes possibles).
Je classe cet article dans les « paradoxes » en ce sens que la réponse est vraiment contre-intuitive !
Combien de mélanges possibles pour 3 cartes ?
Commençons par étudier un cas plus simple, celui d’un jeu composé de 3 cartes : une dame D, un as A et un roi R.
Pour lister les différents mélanges, écrivons-les : D R A / D A R / A D R / A R D / R D A / R A D. Les 2 premiers sont représentés ci-contre.
On en compte 6.

C’est ici que la réflexion mathématique est intéressante. Nous allons voir comment dénombrer ces mélanges plus facilement, et faire apparaitre une formule. Dans notre cas de 3 cartes, tentons de construire un mélange complètement hasardeux : j’ai 3 possibilités pour la première carte. Une fois qu’elle est choisie, je n’ai plus que 2 possibilités pour la deuxième. Et enfin, je n’ai plus le choix, la troisième est la seule restante.
Cela nous donne en tout : 3 × 2 × 1 = 6 mélanges.
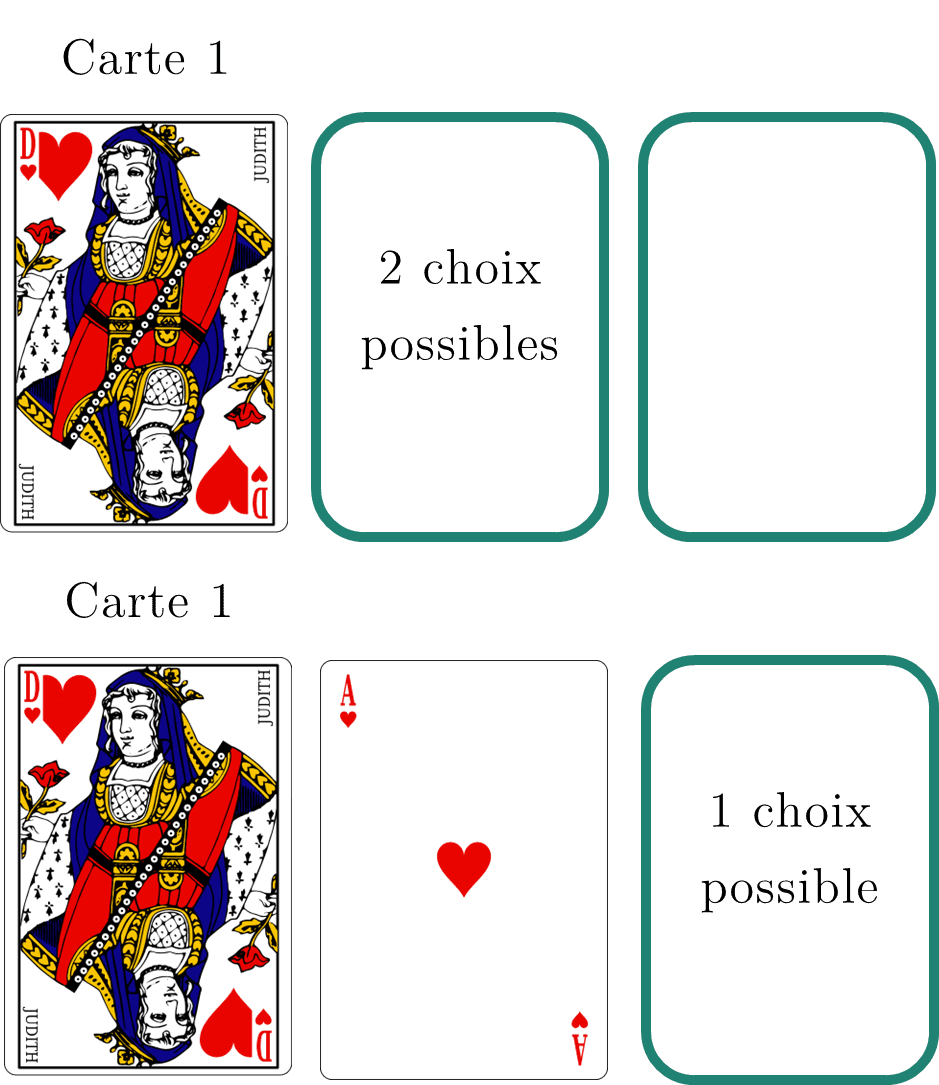
Il faut bien comprendre pourquoi nous multiplions : lorsque je choisis la 1ère carte, j’imagine 3 « mondes parallèles » (un pour D, un pour R, un pour A en fonction de la carte choisie). Dans chacun de ces mondes, il y a autant de façons de mélanger les cartes restantes.
Combien de mélanges possibles pour 52 cartes ?
Faisons un petit bilan sur notre façon de mélanger. Chaque carte doit apparaitre exactement une fois dans le mélange. En mathématiques, nous appelons ça une permutation. Cela correspond bien au sens du mot : on part d’un mélange quelconque, on permute un certain nombre de cartes pour en obtenir un nouveau.
Il n’est pas difficile de compter les permutations. Comme vu précédemment, pour 3 cartes il faut compter 3 × 2 × 1.
En fait, ce procédé se généralise aisément. Pour 4 cartes : on choisit la 1ère (4 choix) puis la deuxième (3 choix), la troisième (2 choix) et la dernière (1 choix). Ceci donne 4 × 3 × 2 × 1 = 24 possibilités.
Pour simplifier cette écriture, nous notons 4 ! = 4 × 3 × 2 × 1 et on lit « factorielle n » (non, le point d’exclamation n’est pas là pour signifier qu’il faut CRIIIER 4).
De façon générale, on note pour en entier n : n ! = n × (n-1) × … × 3 × 2 × 1.
Avec la façon de compter utilisée, nous savons qu’il y a donc 52 ! mélanges d’un jeu de 52 cartes.
Oui, mais 52 !, cela fait combien ? Je vous le donne :
80658175170943878571660636856403766975289505440883277824000000000000, soit environ 8.0658175e+67.
Oui oui ! Cela est absolument gigantesque !
Pour comparaison, on estime à 10^50 le nombre d’atomes sur Terre. Il y a plus de mélanges possibles de 52 cartes que d’atomes sur Terre : c’est vertigineux !
Moralité : méfiez-vous de l’intuition en dénombrement. Ceci est à la base de bon nombre de supercheries (comme le loto) : nous y reviendrons plus tard !


Commentaires récents