Voici une petite énigme liée à un trajet en voiture ! Avant de vous présenter l’énoncé, je vais vous donner 2 consignes ! La première : tentez de donner une réponse « intuitive » (voire plusieurs !) au problème. Puis prenez le temps de trouver la réponse par vous-même (pour cela : munissez-vous de papier et d’un crayon !).
Voici la situation : « Vous effectuez un trajet Paris – Marseille en voiture, soit 1 000 km. Vous vous arrêtez à mi-chemin et constatez que vous avez roulé à une vitesse moyenne de 100 km/h. Quelle doit être votre vitesse sur le reste du trajet pour avoir une vitesse moyenne de 200 km/h sur l’ensemble du trajet ? ».
L’énoncé est fictif, notamment les vitesses mises en jeu. Bien évidemment : on respecte les limitations au volant !

Solution de l’énigme
Pour commencer, rappelons qu’une vitesse est le rapport entre la distance et le temps : v = d/t (d’où l’unité des km/h : la distance divisée par le temps). De cette formule, nous pouvons exprimer le temps par : t = d/v.
Dans notre problème, calculons le temps mis pour faire la première moitié du trajet soit 500km : t = d/v = 500/100 = 5.
A mi-chemin, nous avons roulé 5h.
Calculons maintenant le temps que l’on doit mettre pour faire l’ensemble du trajet, soit 1 000km à une vitesse moyenne de 200 km/h : t = d/v = 1 000/200 = 5h.
Il faut donc rouler 5h pour faire le trajet entier à 200 km/h.
Oups ! A mi-chemin, nous avons déjà roulé 5h… En fait, il faudrait se téléporter instantanément… Quel que soit votre vitesse, vous ne pourrez pas satisfaire le problème ! Même la lumière et ses 300 000 km/s (par secondes !) sont insuffisants !
Les calculs sont formels. Je suis persuadé que si vous ne connaissiez pas ce problème, il vous a surpris ! Avouez que cela n’est pas du tout intuitif (d’ailleurs : comparez avec votre intuition de départ !).
Je vous propose de creuser un peu ces histoires de vitesses moyennes.
Moyennes de vitesses
Dans cette partie, il y aura quelques calculs. Pas forcément méchants, mais je comprends que cela puisse rebuter. Vous pouvez donc lire l’article sans vous préoccuper des calculs !
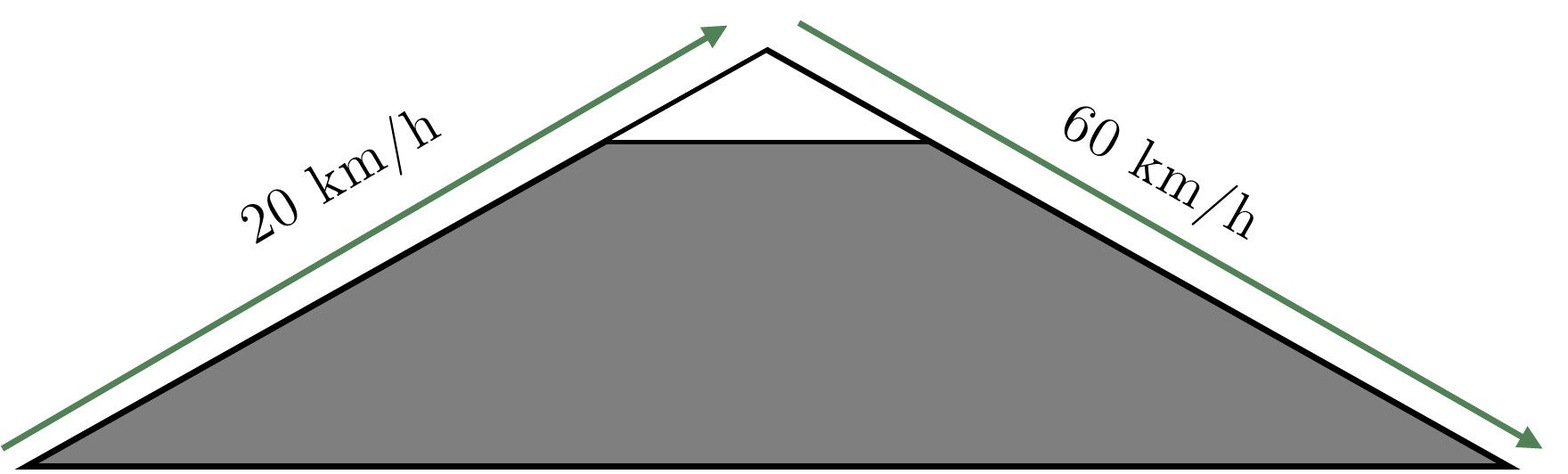
Partons d’un nouveau problème. Vous montez un col à vélo à une vitesse moyenne v1 de 20 km/h. Une fois en haut, vous redescendez à une vitesse v2 de 60 km/h.
Quelle est votre vitesse moyenne sur l’ensemble de votre parcours ? Notez qu’ici, on ne connait pas la distance parcourue (cela ne change rien à la question, vous verrez !). On va noter d la distance pour monter au col. Pour redescendre, la distance est aussi de d.
Lançons-nous ! Pour connaitre la vitesse moyenne, nous devons connaitre :
1. La distance parcourue : d à l’aller et d au retour, donc 2d en tout.
2. Le temps de trajet :
- A l’aller : on parcourt la distance d à 20 km/h. On a donc : t1 = d/v1 = d/20
- Au retour : on parcourt d à 60 km/h. On a donc : t2 = d/v2 = d/60
- Temps total : d/20 + d/60
On calcule alors la vitesse moyenne :
$ = \dfrac{2d}{\dfrac{d}{20}+\dfrac{d}{60}}$
$ = \dfrac{d}{\dfrac{1}{20}+\dfrac{1}{60}}$ On simplifie par d
$ = \dfrac{2}{\dfrac{80}{1200}}$ On réduit au même dénominateur
$= \dfrac{2 × 1200}{80}$
$ = 30$
Le cycliste a donc roulé à une vitesse moyenne de 30km/h.
Remarquez bien que cette valeur moyenne n’est pas celle dont nous avons l’habitude. Généralement, lorsque l’on pense moyenne de 20 et 60 on calcule (20+60)/2 = 40 : on appelle cela la moyenne arithmétique. C’est celle que l’on utilise pour connaitre notre moyenne à l’école !
Pour des vitesses, la moyenne utilisée est dite harmonique. Si l’on prend 2 nombres a et b, leur moyenne harmonique est définie par : 2/(1/a + 1/b).
Ceci correspond exactement au problème du cycliste ! La vitesse moyenne lors d’un trajet aller à la vitesse v1 et la vitesse v2 au retour est donné par la moyenne harmonique des vitesses : 2/(1/v1 + 1/v2).
Pour vérifier cette formule générale, il s’agit essentiellement de faire les calculs déjà faits dans l’exemple du cycliste. Je vous laisse le soin de le faire par vous-même si l’envie vous prend !
Il est assez intéressant de noter comme annoncé que cela est indépendant de la distance parcoure !
L’énigme via la moyenne harmonique
Revenons à notre problème initial et traitons-le à l’aide de notre nouvelle formule.
Ici, la première vitesse est de 100 km/h et nous voulons une vitesse moyenne de 200 km/h. Comme nous le savons maintenant, la distance de trajet n’est pas importante. Traduisons cela en équation.
Nous cherchons la vitesse v sur la deuxième moitié du trajet telle que la moyenne harmonique de 100 et de v soit égale à 200 :
$ \Leftrightarrow \dfrac{2}{\dfrac{v+100}{100v}}=200$
$ \Leftrightarrow \dfrac{200v}{v+100}=200$
$ \Leftrightarrow 200v=200v+20000$
$ \Leftrightarrow 0=20000$
Ceci signifie que notre équation de départ est équivalente à l’équation 0 = 2000. Autrement dit, aucune vitesse v ne peut satisfaire l’égalité (sinon cela équivaudrait à 0 = 2000). Il n’y a pas de réponse à notre problème, comme nous le savions déjà !
En conclusion, j’aimerais insister sur cette nouvelle moyenne dite harmonique. Ce problème de vitesse nous a permis d’aboutir à cette jolie formule, que l’on présente rarement dans la scolarité ! Sachez qu’il existe encore d’autres moyennes (quadratique, géométrique…) et qu’elles apparaissent dans des situations bien concrètes. Il faudra que je prenne le temps de vous les présenter !
Petits compléments
1. Voici la formule qui donne la moyenne harmonique de k nombres (tous strictement positifs) n1, n2, …, nk :
Attention, tous les nombres doivent être strictement positifs. En effet, si l’un est négatif cela n’a pas de sens pour la vitesse. Si l’un est cela cela est aussi problématique pour la vitesse (on avance pas…). Mais cela engendre un problème plus grave : une division par 0 dans la formule. Et ça… c’est le pire des cataclysmes ! Vous pouvez vous référer à mon article suivant :
2. Sur l’exemple du cycliste nous avons vu que la moyenne harmonique de 20 et 60 vaut 30. Cette valeur est inférieure à la moyenne arithmétique qui vaut 40. On peut se demander si c’est toujours le cas : la réponse est oui (sauf dans le cas a = b ou les 2 moyennes sont égales). Pour le montrer, on peut résoudre une inégalité entre la moyenne harmonique de 2 nombres a et b d’un côté, et leur moyenne arithmétique de l’autre.
En un certain sens, les vitesses les plus faibles « comptent plus » que les grandes vitesses lorsque l’on calcule la vitesse moyenne.


Commentaires récents